VideoCrafter
Model composition
Introducing the cast of VideoCrafter:
How to Use VideoCrafter
There are a couple of ways you can play around with VideoCrafter. You can run it locally, run a demo on HuggingFace, the Google Colabatory notebook or on Replicate.
Prompt engineering : prompt engineering is the most important parameter when it comes to generative models. A good resource to understand this is here .
The HuggingFace demo of VideoCrafter shows us the features we have available to play around with.
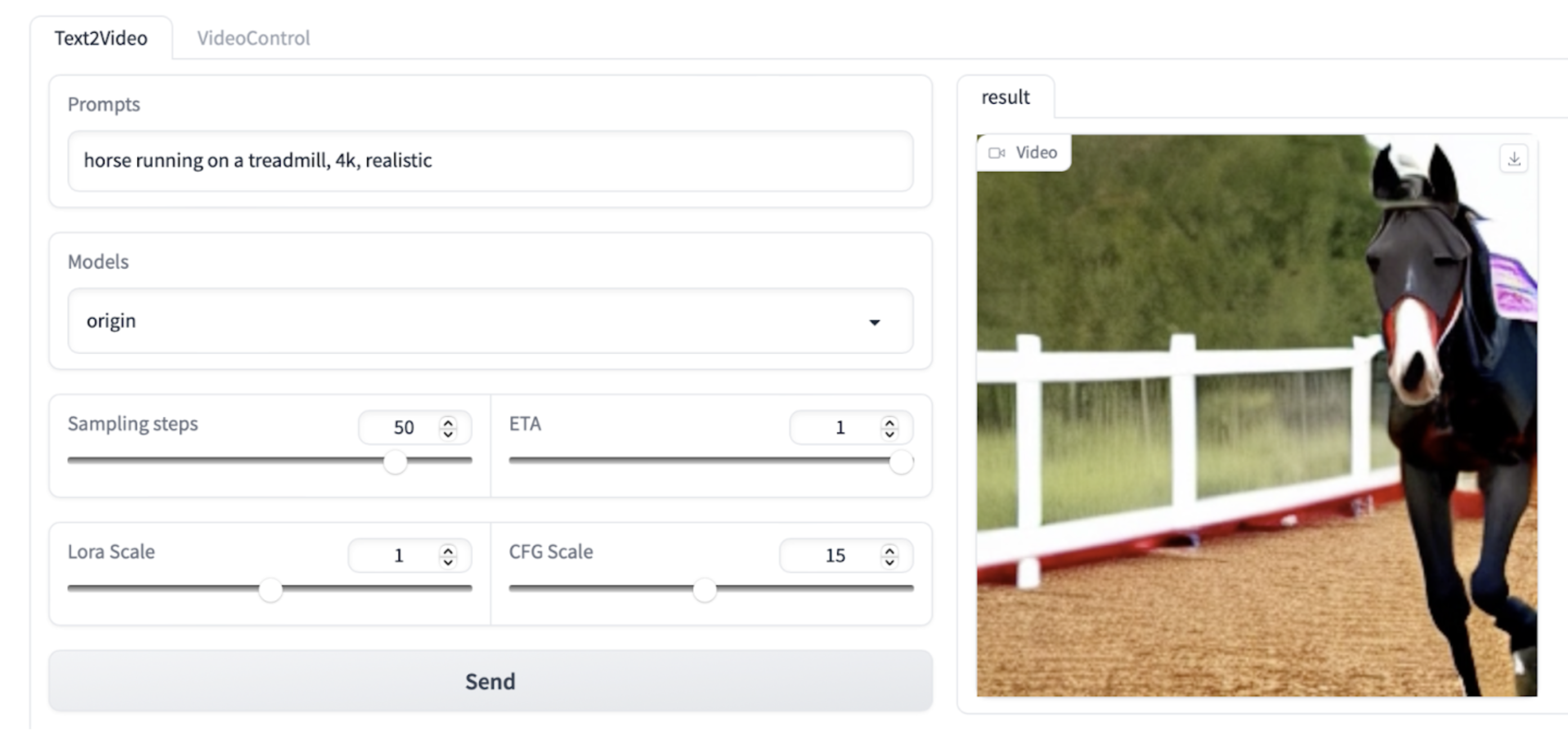
Prompt: "teddy bear playing the piano, high definition, 4k", all other settings default
1 sampling step
10 sampling step
50 sampling step
LoRA demonstration; Prompt : "black cat eating ice cream, animated", sampling steps = 50
Default model
Frozen movie style, LoRA 1.6
Vincent Van Gogh style, LoRA 1.6
Vincent Van Gogh style, LoRA 2
Diffusion models
Diffusion models are among the more mathematically involved generative models. For more explanation on the math behind these models, see this doc.
Latent diffusion models are a type of machine learning model that map the characteristics of a dataset to a lower-dimensional latent space through an encoder.
A key intuition when considering how machine learning models is : it is desired that every arbitrary data sample can be represented by a well-understood distribution so that established properties can be used to make computations more efficient.
Diffusion models "generate" by "diffusing" an existing image of a certain class into complete noise, and then un-diffusing it into a sensible sample. This ends up generating a new image as the calculations are approximate and we make smart assumptions to preserve the structure of the image while making calculations more efficient.
In an attempt to make this less hand-wavey, let's take a bird-eye's view of the mathematics.
We have a data point which we will use to convert into an image of the same category.
Let's say this data point, x_0 resembles a distribution q(x). We assume that the process of adding noise to this distribution is a Markovian process, and we model it by q(x_t | x_{t-1}).
We fix a variance schedule, {β} that influences the variance in the noisiness between timesteps. We fix T of these, where T is the chosen number of sampling steps. By the end of this forward process, we've converted the sample to pure noise.
We can now start generating a never-seen-before image out of this noise. If we try to take the posterior of the previous Markovian process, if the covariance between the distributions at two consecutive timesteps is small enough, it can be shown that the posterior follows approximately the same distribution as the original process. Thus we have an approximate posterior, called p(x_{t-1} | x_t), and the real distribution q(x_{t-1} | x_t). We will leverage the distribution p(x_t) till we can remove all the noise from the sample and resolve it to a new image. Different diffusion models use different models of p. If we try to model p as close to q as possible, p would be a Markovian process as well and be computationally heavy. This is the concept of Denoising Diffusion Probabilistic Models (DDPM). Denoising Diffusion Implicit Models, as used in VideoCrafter, ease computational complexity by assuming a non-Markovian reverse process distribution.
The training objective of diffusion models is an optimisation function comparing the approximate distribution p and the actual reverse distribution q. Since we cannot possibly compute the real values of these effectively, we use a variational lower bound (as in VAEs), using KL Divergence and cross-entropy. If you wish to learn more about this, you may want to check out this link and then this one.
Inferences
In my observations with VideoCrafter, it does a good job of rendering simple prompts. Diffusion models in general seem to be good at identifying and generating images around one main subject and unless in simple cases, fail to generate multiple complex elements. This would make sense considering the mechanism as explained above.
VideoCrafter has the interesting feature of allowing long-form video generation. The mechanisms used to achieve this are interesting, as typically diffusion models fail for longer form content generation. Using autoregressive latent prediction and unconditional guidance, techniques which are further described in the original LVDM paper.
References
He, Y., Yang, T., Zhang, Y., Shan, Y. & Chen, Q. 2023 Latent Video Diffusion Models for High-Fidelity Long Video Generation. arXiv:2211.13221 https://arxiv.org/abs/2211.13221
Goodfellow, I., Pouget-Abadie, J., Mirza M., Xu, B., Warde-Farley, D., Qzair, S., Courville, A. & Bengio, Y. 2014 General Adversarial Networks arXiv:1406.2661 https://arxiv.org/abs/1406.2661
Feller, W. 1949 On The Theory of Stochastic Processes With Particular Reference to Applications Project for Research in Probability
Sohl-Dickstein, J., Weiss, E., Maheswaranathan, N., & Ganguli, S. 2015 Deep Unsupervised Learning using Nonequilibrium Thermodynamics arXiv:1503.03585 https://arxiv.org/abs/1503.03585
Blattman, A., Rombach, R., Ling, H., Dockhorn, T., Kim, S., Fidler, S. & Kreis, K. 2023 Align Your Latents. IEEE Conference on Computer Vision and Pattern Recognition. arXiv:2304.08818 https://arxiv.org/abs/2304.08818
Graikos, AYellapragada S. & Samaras, D. 2023 Conditional Generation from Unconditional Diffusion Models using Denoiser Representations. arXiv:2306.01900 https://arxiv.org/pdf/2306.01900.pdf
